4. Les comportement à l’origine de ![]()
1. Les limites de référence : Résultats du cours ( démontrés ou admis )
2. Les opérations sur les limites.
3. La croissance comparée des fonctions logarithme, exponentielle et puissances.
4. Les comportement à l’origine de
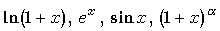
5. Des méthodes de calcul en cas de F.I. ( Formes indéterminées ).
6. Les théorèmes de comparaisons.
EXERCICE : Des exercices corrigés pour s’entraîner
rem 1 : La démarche doit toujours figurer clairement en indiquant soit que le résultat est connu d’après le cours, soit en faisant apparaître l’une des méthodes indiquées au paragraphe 5.
rem 2 : La rigueur de la justification tient au fait que l’élève est capable de déceler si la limite est connue, si son calcul est la conséquence d’une opération ou s’il doit aller plus loin dans sa recherche en utilisant l’une des méthodes indiquées au 5.
Fiche n°1 : Polynômes.
Fiche n°2 : Fonctions rationnelles.
Fiche n°3 : Fonctions comportant des radicaux.
Fiche n°4 : Fonctions comportant des logarithmes.
Fiche n°5 : Fonctions comportant des exponentielles.
1. Limites de référence
Les limites de référence sont toutes les limites connues sur les fonctions de base du cours :
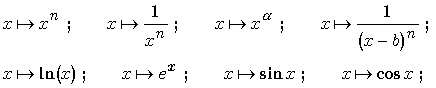
Puissances entières :
Puissances réelles :
Logarithme et exponentielle :
Fonctions trigonométriques
2. Opérations sur les limites
Somme
| lim f | lim g | lim f + g | |
| L | L' | L+ L' | |
| L | + ¥ | + ¥ | |
| L | - ¥ | - ¥ | |
| + ¥ | + ¥ | + ¥ | |
| - ¥ | - ¥ | - ¥ | |
| + ¥ | - ¥ | F I | Forme indéterminée ¥ - ¥ |
Produit
| lim f | lim g | lim f x g | |
| L | L’ | L x L’ | |
| L ¹ 0 | ¥ | ¥ | 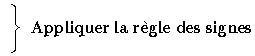 |
| ¥ | ¥ | ¥ | |
| 0 | ¥ | F I | Forme indéterminée 0 ´ ¥ |
| lim f | lim g | lim f / g | |
| L | L’ ¹ 0 | L / L’ | |
| L ¹ 0 | 0 | ¥ | Appliquer la règle des signes |
| 0 | 0 | F I | |
| L | ¥ | 0 | |
| ¥ | L' | ¥ | |
| ¥ | ¥ | F I |
Racine
| lim f | lim f |
| L ³ 0 | |
| + ¥ | + ¥ |
Fonction composée :
3. Croissance comparée
Il s’agit de comparer les limites en +
¥ des fonctions logarithmes, exponentielles et puissancesOn en déduit les autres limites suivantes :
4. Comportement à l’origine
5. Méthodes de calcul
Polynôme
P1 :
P2 : En + ¥ et en - ¥ un polynôme se comporte comme son terme de plus haut degré.
Fonction rationnelle
P3 :
.
P4 : En + ¥ et en - ¥, une fonction rationnelle se comporte comme le quotient des termes de plus haut degré
P5 :
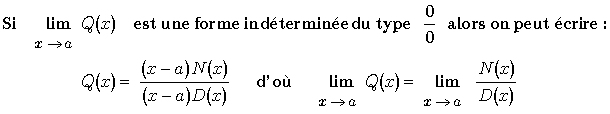
Expression comportant des radicaux
P6 : En présence d’une forme indéterminée avec des radicaux il faut transformer le terme comportant un radical qui pose problème.
Deux solutions sont possibles
Entrer un nombre sous le radical ( ATTENTION AU SIGNE ).
Produit par l'expression conjuguée.
6. Théorèmes de comparaison
f est une fonction définie sur un intervalle I ;
![]()
Théorème 1 :
Théorème 2 : f et g sont définies sur I.
conséquences du th 2 :
Th 3 : ( Th des gendarmes ou d’encadrement )
Th 4 :
Commentaires
3. Croissance comparée
Ces limites résultent du fait que :
La fonction logarithme népérien croît beaucoup moins rapidement que toute fonction puissance.
Toute fonction puissance croît moins rapidement que la fonction exponentielle.
Ces résultats s'observent sur le graphique ci-dessous :
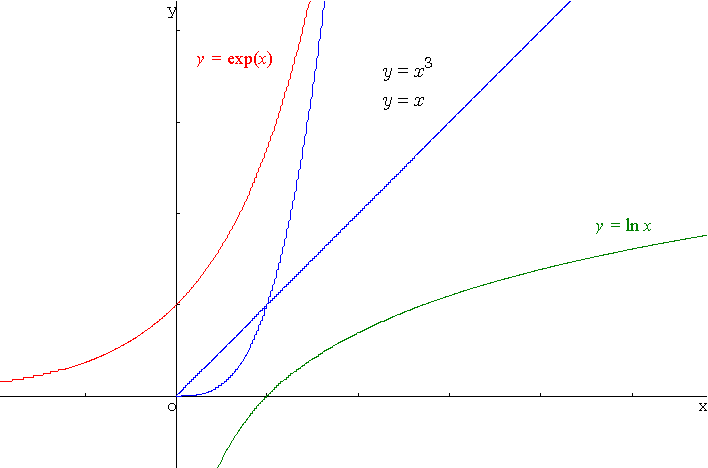
4. Comportement à l’origine
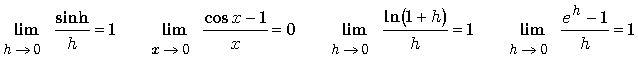
Ces limites sont obtenues à l'aide de formules de dérivées de fonctions connues :