

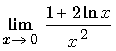
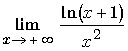
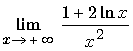

Avant de regarder les réponses prenons une feuille de papier et cherchons.
Pour voir la réponse cliquer sur l'énoncé.
| L 1 : | L 6 : | ||
| L 2 : | L 7 : |  |
|
| L 3 : |  |
L 8 : | |
| L 4 : | 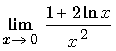 |
L 9 : | 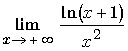 |
| L 5 : | 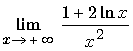 |
L 10 : |  |
L 1 :
Pas de problème, on calcule la limite de chacun des termes et l'on obtient la réponse.
Réponse : Voir Corrigé 1
L 2 :
Ici, on trouve une forme indéterminée du type ¥ - ¥.
Songer à utiliser la propriété :
Réponse : Voir corrigé 2
L 3 :

. C'est un résultat du cours. ( croissance comparée )
S'écrit
. Il suffit d'appliquer les opérations sur les limites.
Réponse : Voir Corrigé 3
L 4 :

Songer à écrire
.
Utiliser les opérations sur les limites.
Réponse : Voir Corrigé 4
L 5 :

Songer à écrire
.
Utiliser la croissance comparée
Réponse : Voir Corrigé 5
L 6 :
![]()
On obtient une forme indéterminée du type ¥ - ¥.
Il faut donc transformer l'expression en mettant ln x en facteur.
Réponse : Voir Corrigé 6
L 7 :

Ces deux limites donnent une forme indéterminée du type ¥ - ¥.
Il faut transformer l'expression en factorisant au numérateur et au dénominateur par ln x, puis simplifier.
Réponse : Voir Corrigé 7
L 8 :
![]()
Il faut factoriser par x pour ne pas avoir de forme indéterminée.
Réponse : Voir Corrigé 8
L 9 :

Pour pouvoir utiliser la croissance comparée, il faut écrire :
. Le premier terme est alors de la forme
Réponse : Voir corrigé 9
L 10 : .

rem 1 : Il faut lire
.
rem 2 : Il s'agit de limites de fonctions composées ln o u avec
Réponse : Voir Corrigé 10
C 1 :
C 2 :
Remarque : Dans un devoir, la première partie n’est pas rédigée sur la copie mais seulement cherchée au brouillon.
C 3 :
C 4 :
C 5 :
C 6 :
C 7 :
C 8 :

C 9 :

C 10 :