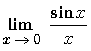
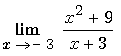
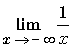
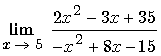
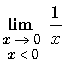
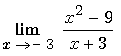
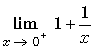
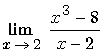
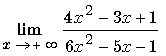
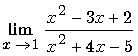
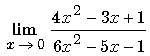
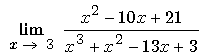
Avant de regarder les réponses prenons une feuille de papier et cherchons.
Pour voir la réponse cliquer sur l'énoncé.
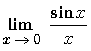 |
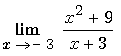 |
|
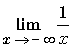 |
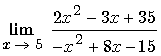 |
|
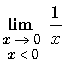 |
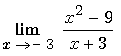 |
|
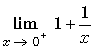 |
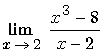 |
|
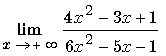 |
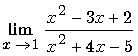 |
|
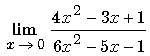 |
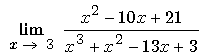 |
![]() : C'est une fonction de référence. Donc
: C'est une fonction de référence. Donc ![]() = + ¥
= + ¥
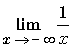 : C'est une fonction de
référence. Donc
: C'est une fonction de
référence. Donc 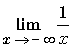 =
0
=
0
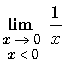 : Forme L / 0. Le signe est négatif
car : 1 est positif et x est négatif .
: Forme L / 0. Le signe est négatif
car : 1 est positif et x est négatif .
Donc 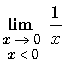 = - ¥
= - ¥
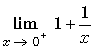 : Forme L / 0. Le signe est positif
car : 1 est positif et x ® 0+ signifie x
> 0.
: Forme L / 0. Le signe est positif
car : 1 est positif et x ® 0+ signifie x
> 0.Donc
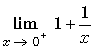 = + ¥
= + ¥
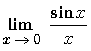 : Comportement à
l'origine. Donc
: Comportement à
l'origine. Donc 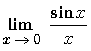 = 1
= 1
![]() : Forme ( + ¥) + (+ ¥).
Donc
: Forme ( + ¥) + (+ ¥).
Donc ![]() = + ¥
= + ¥
![]() F.I ¥-¥. Il faut utiliser une
méthode particulière.
F.I ¥-¥. Il faut utiliser une
méthode particulière.
Cours : Voir P 2
Réponse : Voir Lim P 1
![]() :
Remplacer x par 2 et calculer
:
Remplacer x par 2 et calculer ![]() .
.
Donc ![]() = - 3
= - 3
![]() : Remplacer x par 0. Donc
: Remplacer x par 0. Donc ![]() = 9
= 9
![]() : F.I ¥-¥. Il faut
utiliser une méthode particulière.
: F.I ¥-¥. Il faut
utiliser une méthode particulière.
Cours : Voir P 2
Réponse : Voir Lim P 2
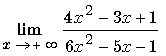 : F.I ¥/¥. Il
faut utiliser une méthode particulière.
: F.I ¥/¥. Il
faut utiliser une méthode particulière.
Cours : Voir P 4
Réponse :Voir lim F 3
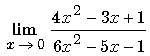 : Remplacer x par 0. Donc
: Remplacer x par 0. Donc 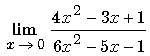 = -1
= -1
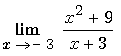 :
: ![]()
Il faut étudier le signe de x + 3 au voisinage de –3.
Cours : Voir opération quotient
Réponse : Voir lim F 4
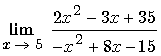 :
: ![]()
Il faut étudier le signe de – x2 + 8x –15 au voisinage de 5.
Cours : Voir opération quotient
Réponse : Voir Lim F 5
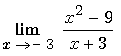 : F.I 0 / 0 . On ne peut
pas remplacer x par -3. Le calcul n’est pas
possible.
: F.I 0 / 0 . On ne peut
pas remplacer x par -3. Le calcul n’est pas
possible.
Il faut utiliser une méthode particulière.
Cours : Voir Méthode fonction rationnelle
Réponse : Voir Lim F 6
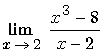 : F.I 0 / 0 . On ne peut
pas remplacer x par
: F.I 0 / 0 . On ne peut
pas remplacer x par
Il faut utiliser une méthode particulière.
Cours : Voir Méthode fonction rationnelle
Réponse : Voir Lim F 7
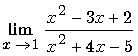 :
F.I 0 / 0 . On ne peut pas remplacer x par 1. Le calcul
n’est pas possible.
:
F.I 0 / 0 . On ne peut pas remplacer x par 1. Le calcul
n’est pas possible.
Il faut utiliser une méthode particulière.
Cours : Voir Méthode fonction rationnelle
Réponse : Voir lim F 8
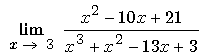 :
F.I 0 / 0 . On ne peut pas remplacer x par 3. Le calcul
n’est pas
:
F.I 0 / 0 . On ne peut pas remplacer x par 3. Le calcul
n’est pas
possible.Il faut utiliser une méthode particulière.
Cours : Voir Méthode fonction rationnelle
Réponse : Voir Lim F 9
P 1 :
On peut mettre x2 en facteur pour obtenir une forme ¥ ´ ¥
P 2 :
¥´ 1.Méthode : mettre en facteur le terme de plus haut degré.
On obtient alors une forme
rem : On constate que, puisque le terme entre parenthèse à pour limite 1 que le polynôme se comporte comme son terme de plus haut degré. Ce qui autorise à écrire la forme synthétique suivante :
Attention, cette méthode n’est valable qu’en +¥ et en -¥.
F 3 :
On applique au numérateur et au dénominateur la propriété des polynômes en + ¥
Remarquer à la troisième égalité la disparition du terme " lim " car il y a eu simplification par x2 et l’absence de variable permet de ne plus écrire ce terme.
F 4 :
La forme 18/0 exige l’étude du signe de x+3. On va donc présenter un tableau de signe au dessous duquel on indiquera les divers résultats
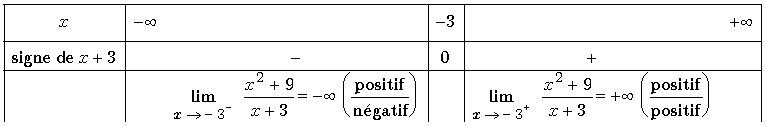
F 5 :
La forme 70/0 exige l’étude du signe de – x2 + 8x – 15 .
Le calcul de delta fait apparaître deux racines distinctes 3 et 5.
L’expression est du signe – à l’extérieur de l’intervalle des racines.
Remarque :
En 5 - , c’est à dire à gauche de 5, le dénominateur est positif et le numérateur aussi.
En 5 +, c’est à dire à droite de 5, le dénominateur est négatif et le numérateur positif.
F 6 :
Puisque l’on a une forme 0/0, cela signifie que - 3 est une racine commune au numérateur et au dénominateur
En factorisant ceux ci par (x+3) on va pouvoir effectuer une simplification.
F 7 :
Puisque l’on a une forme 0/0, cela signifie que 2 est une racine commune au numérateur et au dénominateur.
En factorisant ceux ci par (x - 3 ) on va pouvoir effectuer une simplification.
Remarque : La factorisation doit être justifiée. On peut utiliser :
La méthode de Horner,
La division de polynômes,
La méthode d’identification.
F 8 :
Puisque l’on a une forme 0/0, cela signifie que 1 est une racine commune au numérateur et au dénominateur.
En factorisant ceux ci par (x - 1 ) on va pouvoir effectuer une simplification.
Remarque : Les factorisations doivent être justifiées.
F 9 :
Puisque l’on a une forme 0/0, cela signifie que 3 est une racine commune au numérateur et au dénominateur.
En factorisant ceux ci par (x-3) on va pouvoir effectuer une simplification.
Remarque : Les factorisations doivent être justifiées