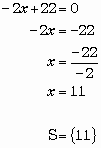
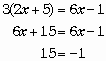
égalité fausse
S = { } ou S = Æ
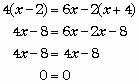
égalité vraie
S =
réquation
1. Egalité et équation
|
4 + 1 = 5 égalité vraie |
2 + 3 = 6 égalité fausse |
(x+1) 2 = x2 + 2x + 1 Egalité vraie Pour tout réel x |
3 + 2x = 8 égalité vraie ou fausse selon la valeur de x |
Def :
Une équation c'est une égalité comportant une variable et dont on ne sait pas si elle est vraie ou fausse.Résoudre l'équation, c'est chercher toutes les valeurs de la variable pour lesquelles cette égalité est vraie.
2. Equations de base
Principe : Toute équation peut s'écrire sous la forme d'une expression égale à 0
Définition : Le degré d'une équation c'est l'exposant le plus élevé de la variable
1er cas :
Exemples :
|
|
égalité fausse S = { } ou S = Æ |
égalité vraie S = r |
2ème cas : Produit de facteurs du premier degré nul
Prop 1 : Un produit de facteurs est nul si et seulement si l'un des facteurs est nul.
Exemple :
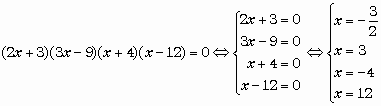
S = { -
4 ; ![]() ; 3 ; 12 }
; 3 ; 12 }
3ème cas : Produit et quotient de facteurs du premier degré nul
Prop 2 : Un quotient est nul si et seulement si son numérateur est nul et son dénominateur est non nul
| Exemple : |
|
On doit avoir |
|
donc |
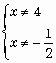
|
|
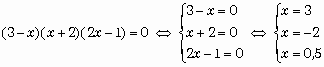
|
Comme aucune de ces trois solutions n'est une valeur interdite au dessus : S = { - 2 ; 0,5 ; 3 }
Prop 3 : Toute équation doit pouvoir se ramener à l'une de ces trois forme.
3. Résolution d'équations
3.1 Reconnaître et classer
| Expressions du premier degré . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | F . . . 1 |
| Expressions comportant une inconnue au dénominateur . . . . . . . . . . | F . . . Q |
| Expressions sans inconnue au dénominateur
. . . . . . . . . . . . . . . . . . . . et d'un degré supérieur à 1 |
F . . . P |
3.2 Transformer pour résoudre
1
Equations du premier degrérem : toute équation du premier degré se ramème à une forme simple en développant et en utilisant les propriétés sur les égalités
Prop 4 : On peut ajouter ou retrancher un même nombre aux deux membres d'une égalité.
Prop 5 : On peut multiplier ou diviser les deux membres d'une égalité par un même nombre non nul.
P
Equations sans inconnue au dénominateur et d'un degré supérieur à 1.Méthode générale : Il faut se ramener à un produit de facteurs nul, en ayant un membre égal à 0 et en factorisant l'autre membre.
Meth 1 : Utiliser une identité remarquable
|
a 2 + 2ab + b 2 = ( a + b ) 2 ; |
a 2 - 2ab + b 2 = ( a - b ) 2 ; |
a 2 - b 2 = ( a + b )( a - b ) |
Meth 2 : Il y a un facteur commun apparent, on factorise après l'avoir mis en valeur
a.b + a.c = a.( b + c )
Meth 3 : Il n'y a pas de facteur commun apparent, Il faut essayer d'en faire apparaître un.
Meth 4 : Si l'on est sûr que les termes d'un degré supérieur à 1 s'éliminent on peut développer
Q
Expressions comportant une inconnue au dénominateurAvant tout calcul, chercher pour quelles valeurs de la variable les expressions sont définies.
Méthode 1 : 1. On se ramène à une équation où l'un des membres est nul.
2. On réduit au même dénominateur ( le plus simple possible ).
3. On factorise le numérateur.
Méthode 2 : Utilisation d'un produit en croix
3. Exercices d'application